GENfarey
"farey" — Fills a table with the Farey Sequence Fn of the integer n.
Description
Plugin gen in fareygen.
A Farey Sequence Fn of order n is a list of fractions in their lowest terms between 0 and 1 and in ascending order. Their denominators do not exceed n. This means a fraction a/b belongs to Fn if 0 ≤ a ≤ b ≤ n. The numerator and denominator of each fraction are always coprime. 0 and 1 are included in Fn as the fractions 0/1 and 1/1. For example F5 = {0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1} Some properties of the Farey Sequence:
- If a/b and c/d are two successive terms of Fn, then bc - ad = 1.
- If a/b, c/d, e/f are three successive terms of Fn, then: c/d = (a+e) / (b+f). In this case c/d is called the mediant fraction between a/b and e/f.
- If n > 1, then no two successive terms ofFn have the same denominator.
The length of any Farey Sequence Fn is determined by |Fn| = 1 + SUM over n (phi(m)) where phi(m) is Euler's totient function, which gives the number of integers ≤ m that are coprime to m.
Some values for the length of Fn given n:
| n | Fn |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 5 |
| 4 | 7 |
| 5 | 11 |
| 6 | 13 |
| 7 | 19 |
| 8 | 23 |
| 9 | 29 |
| 10 | 33 |
| 11 | 43 |
| 12 | 47 |
| 13 | 59 |
| 14 | 65 |
| 15 | 73 |
| 16 | 81 |
| 17 | 97 |
| 18 | 103 |
| 19 | 121 |
| 20 | 129 |
Initialization
size -- number of points in the table. Must be a power of 2 or power-of-2 plus 1 (see f statement).
fareynum -- the integer n for generating Farey Sequence Fn
mode -- integer to trigger a specific output to be written into the table:
-
0 -- outputs floating point numbers representing the elements of Fn.
-
1 -- outputs delta values of successive elements of Fn, useful for generating note durations for example.
-
2 -- outputs only the denominators of the integer ratios, useful for indexing other tables or instruments for example.
-
3 -- same as mode 2 but with normalised output.
-
4 -- same as mode 0 but with 1 added to each number, useful for generating tables for tuning opcodes, for example cps2pch.
Examples
f1 0 -23 "farey" 8 0
Generates generates Farey Sequence F8. The table contains all
23 elements of F8 as floating point numbers.
f1 0 -18 "farey" 7 1
This generates Farey Sequence F7. The table contains 18 delta values of F7,
i.e. the difference between ri+1 - ri, where r is the ith element of Fn.
f1 0 -43 "farey" 11 2
This generates Farey Sequence F11. The table contains the denominators of all
43 fractions in F11.
f1 0 -43 "farey" 11 3
This generates Farey Sequence F11. The table contains the denominators of all
43 fractions in F11, each of those divided by 11, i.e. normalised.
f1 0 -18 "farey" 7 4
This generates Farey Sequence F7. The table contains all fractions of F7,
same as mode 0, but this time '1' is added to each table element.
Example 1320. A simple example of the GENfarey routine.
See the sections Real-time Audio and Command Line Flags for more information on using command line flags.
<CsoundSynthesizer> <CsOptions> </CsOptions> <CsInstruments> sr=44100 ksmps=10 nchnls=1 instr 4 kndx init 0 ; read out elements of F_8 one by one and print to file if (kndx < 23) then kelem tab kndx, 1 fprintks "farey8table.txt", "%2.6f\\n", kelem kndx = kndx+1 endif endin </CsInstruments> <CsScore> ; initialise integer for Farey Sequence F_8 f1 0 -23 "farey" 8 0 ; if mode=0 then the table stores all elements of the Farey Sequence ; as fractions in the range [0,1] i4 0 1 e </CsScore> </CsoundSynthesizer>
Here is a complete example of the GENfarey routine. It uses the files genfarey-2.csd.
Example 1321. Another example of the GENfarey routine.
See the sections Real-time Audio and Command Line Flags for more information on using command line flags.
<CsoundSynthesizer> <CsOptions> ; Select audio/midi flags here according to platform -odac ;;;realtime audio out ;-iadc ;;;uncomment -iadc for RT audio input as well ; For Non-realtime ouput leave only the line below: ; -o genfarey.wav -W ;;; for file output any platform </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 2 0dbfs = 1 ; GENfarey creates table gidelta. ; The table contains the delta values of Farey Sequence 7 (p5=7). ; They are used as Inter Onset Intervals (IOIs) or event durations. ; If p6 is set to 1 for IOI output then the length of the table (p3=-18) is -(|F_7| - 1) ; Remember that a negative sign is for non-power-of-2 table lengths. ; The negative sign in front of the GEN number prevents post-normalisation of its values. gidelta ftgen 0,0,-18,"farey",7,1 ; Use GENfarey with p6 set to 2 to generate the denominators of fractions of F_7 ; this is used in this example as factors to create a series of pitches: gimult ftgen 0,0,-18,"farey",7,2 ;-------- loop and trigger instrument 901 using a Farey Sequence polyrhythm instr 1 kindx init 0 kindx2 init 0 ktrigger init 0 ktime_unit init p6 kstart init p4 kloop init p5 kinitndx init 0 kfn_times init gidelta knote init 60 kbasenote init p8 ifundam init p7 ktrigger seqtime ktime_unit, kstart, kloop, kinitndx, kfn_times if (ktrigger > 0 ) then kpitch = cpspch(ifundam) kmult tab kindx2, gimult kpitch = kpitch * kmult knote = kbasenote + kmult event "i", 901, 0, .4, .10, kpitch, kpitch * .9, 0.4, 5, .75, .8, 1.0, .15, .0, .125, .125, .25, .5, 1.0, .0, .0, .0, .0, .125, .25, .25, .25, knote kindx = kindx + 1 kindx = kindx % kloop kindx2 = kindx2 + 1 kindx2 = kindx2 % kloop endif endin ;------ basic 2 Operators FM algorithm ---------------- instr 901 inotedur = p3 imaxamp = p4 ;ampdb(p4) icarrfreq = p5 imodfreq = p6 ilowndx = p7 indxdiff = p8-p7 knote = p27 aampenv linseg p9, p14*p3, p10, p15*p3, p11, p16*p3, p12, p17*p3, p13 adevenv linseg p18, p23*p3, p19, p24*p3, p20, p25*p3, p21, p26*p3, p22 amodosc oscili (ilowndx+indxdiff*adevenv)*imodfreq, imodfreq, 10 acarosc oscili imaxamp*aampenv, icarrfreq+amodosc, 10 outs acarosc, acarosc endin </CsInstruments> <CsScore> f10 0 4096 10 1 ;sine wave ; p4 kstart := index offset into the Farey Sequence ; p5 kloop := end index into Farey Seq. ; p6 timefac := time in seconds for one loop to complete ; p7 fundam := fundamental of the FM instrument ; p8 basenote:= root pitch of the midi voice output ; note that pitch structures of the midi file output are not equivalent to the ; ones used for the FM real-time synthesis. ; start dur kstart kloop timefac fundam. basenote i1 0.0 44 0 18 2 6.05 60 i1 4 30 0 18 3 7.05 72 i1 34 12 9 18 3 7.05 72 i1 10 12 0 18 1.5 8 84 i1 22 12 0 9 1.5 8 84 i1 15 16 0 18 1 5 48 i1 22 20 5 17 1.7 4 36 i1 46 20 3 11 2.5 7.04 71 i1 51 20 5 13 2.5 7.06 72 i1 73.5 1.5 11 18 1.5 5.05 48 i1 75 1 12 18 1 6.03 58 e </CsScore> </CsoundSynthesizer>
These are the diagrams of the waveforms of the GENfarey routines, as used in the example:
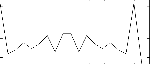
gidelta ftgen 100,0,-18,"farey",7,1 - delta values of Farey Sequence 7

gimult ftgen 101,0,-18,"farey",7,2 - generate the denominators of fractions of F_7